Vectors

go back

Dr Pearce

Some of the images were from my teacher, Dr Pearce.

• Value with Direction and Magnitude

Vector Diagrams

• Vectors can be represented in a diagram
• Arrows are used to represent vector quantities
• Must be some vector on each side
• Must be resolved

Adding Vectors

For 2 Vectors A and B

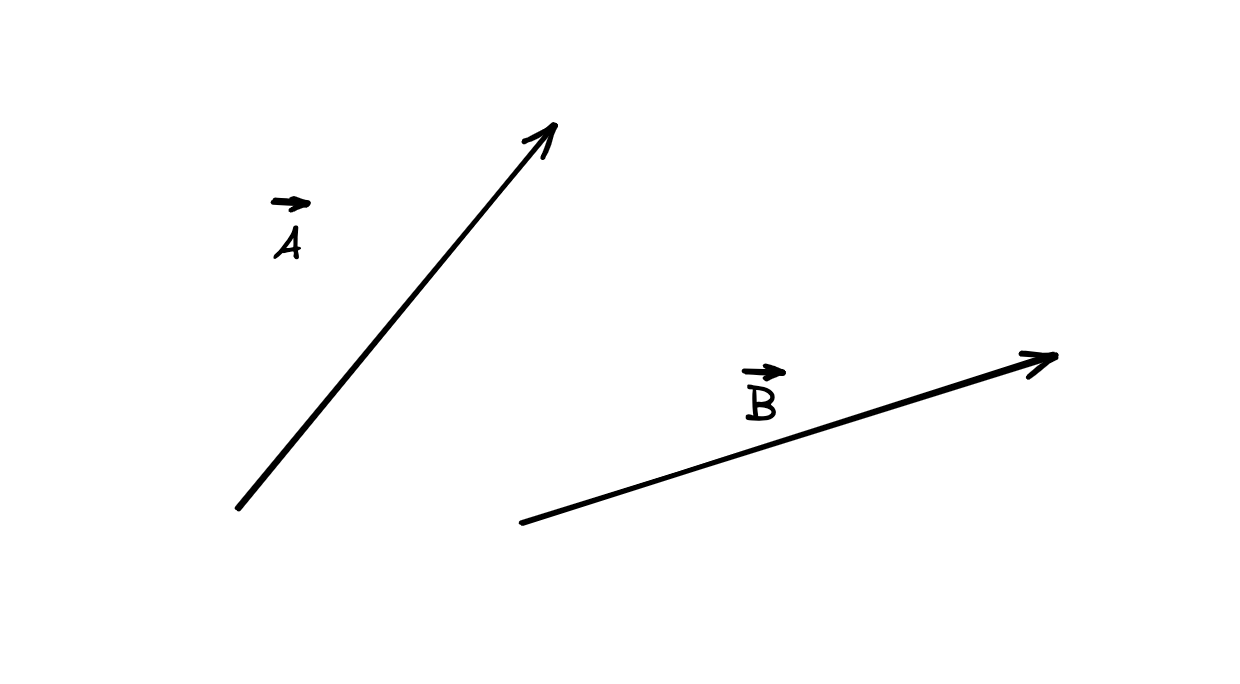
We can use the triangle method:

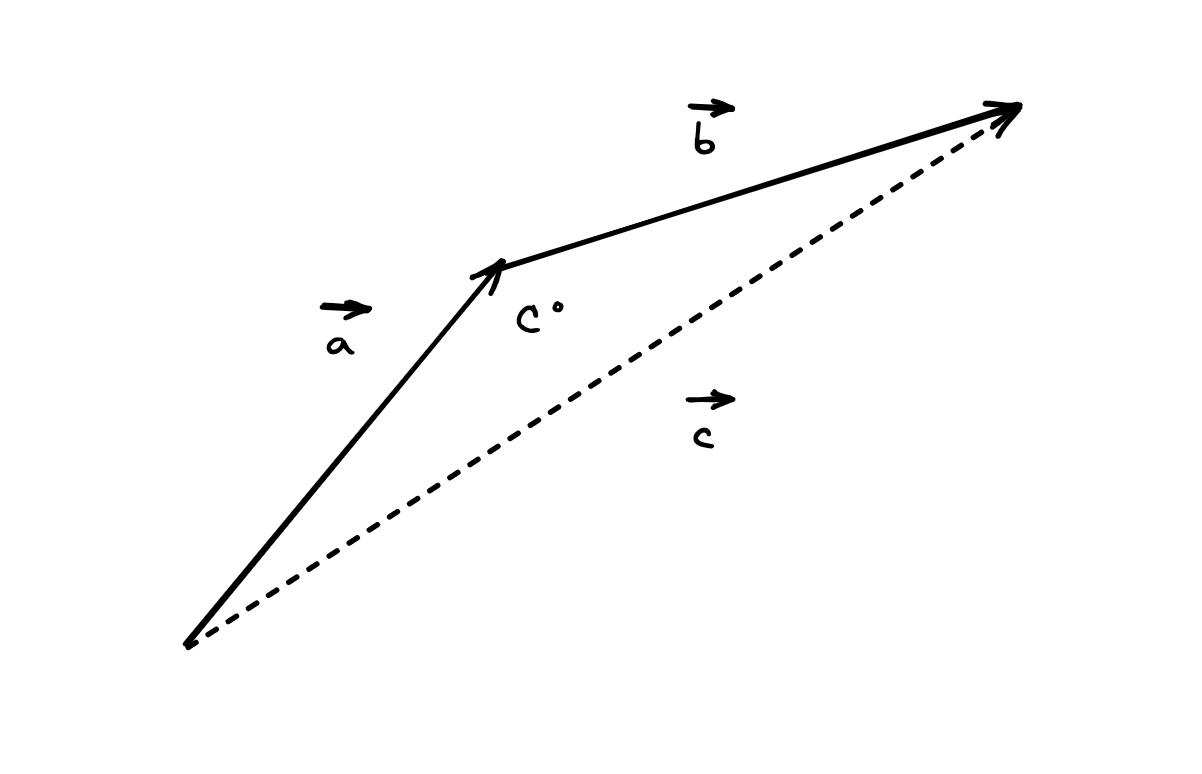
and use the Cosine Rule to find the magnitude of side c:

$c^2=a^2+b^2-2ab\times cos(C)$

and the Sine rule to find the angle it makes from the x axis. They’ll usually give you another angle, to add to this value, as this is not connected to the x or y axis.

$\frac{sin(A)}{a}=\frac{sin(B)}{b}=\frac{sin(C)}{c}$

where the capital letter is the angle opposite the lower-case letter

• E.g., angle A is opposite side a. This also works for the reciprocals of this equation.

We can also use the parallelogram method, and use the methods described above

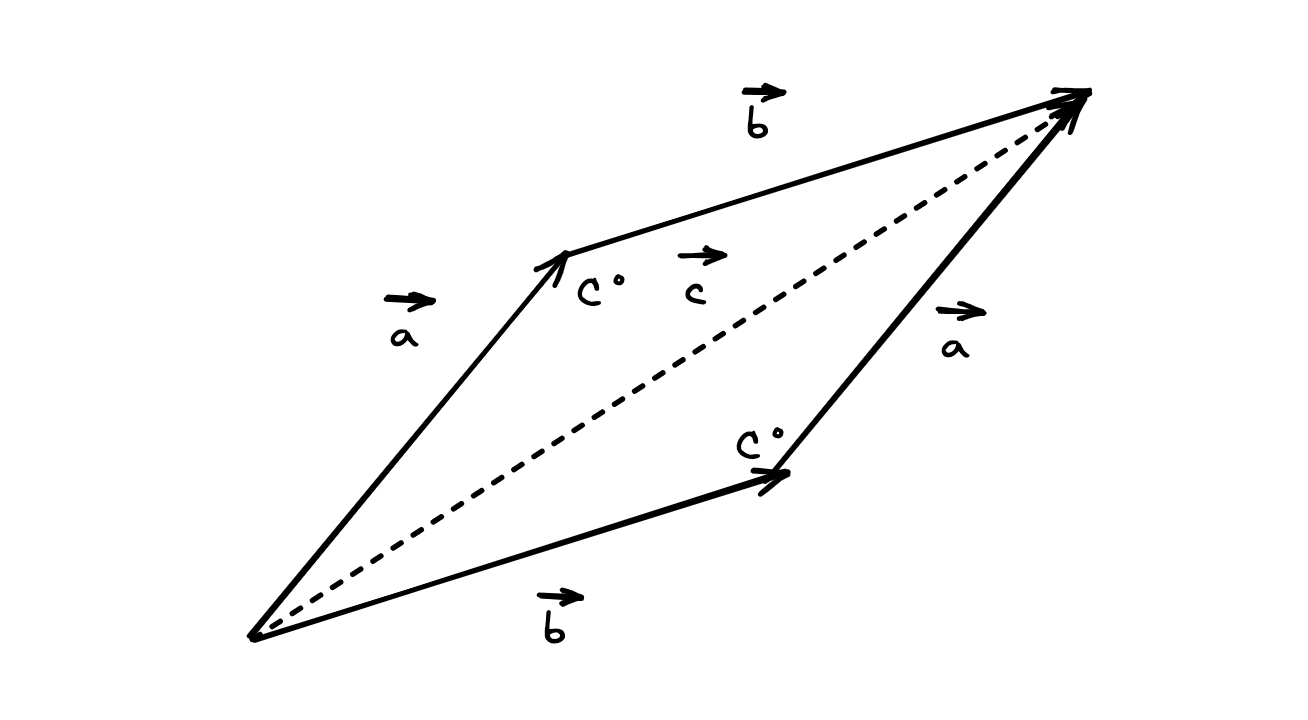There’s also adding Vector Components, but I’ll cover that later

Vectors in Euclidean Geometry

• Line segments are geometrical objects

• $AB$ is the magnitude

• $\overrightarrow{AB}$ is a vector

• $\overline{AB}$ is a line segment

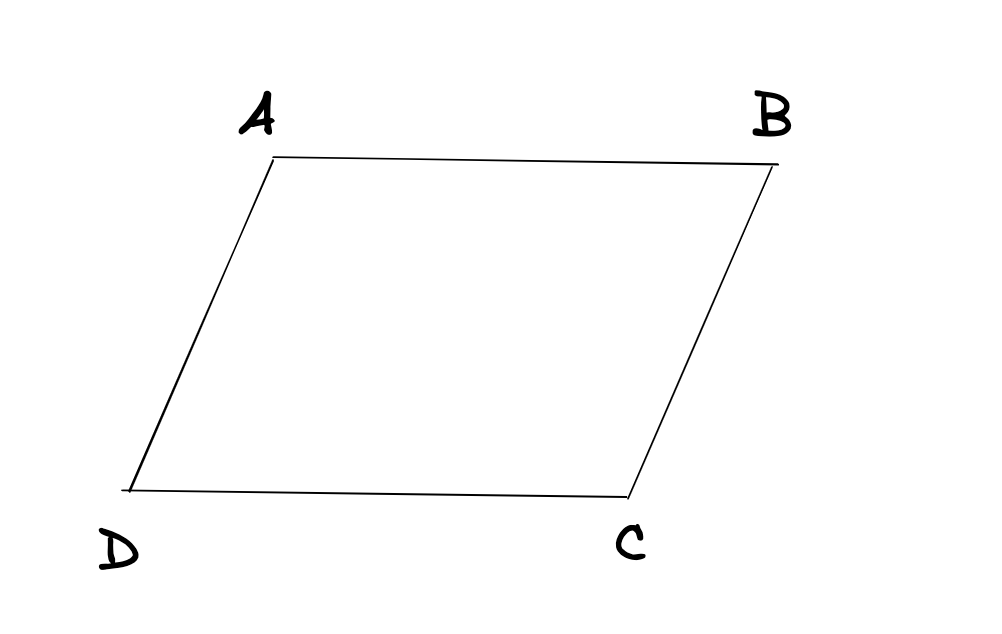
• ABCD is a parallelogram

• $\overline{AD}$ and $\overline{BC}$ are different line segments because, on the cartesian plane, their coordinates are different

  • $\therefore \overline{AD}\ne \overline{BC}$

• $\overrightarrow{AD}$ and $\overrightarrow{BC}$ are the same vector, as they have the same magnitude and direction

  • $\therefore \overrightarrow{AD}=\overrightarrow{BC}$

• Vectors don’t have a fixed location!

• Think of vectors as properties of (directed) line segments

• Addition of vectors in geometry:

$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EF}=\overrightarrow{AF}$

Abstract Vectors

• Vectors can be represented abstractly as mathematical objects which obey certain rules
• They can be notated as lowercase letters in bold
  • a
• Or underlined
  • $\underline{a}$

Mathematical Rules for Abstract Vectors

Equality

• 2 vectors are equal if and only if their magnitudes are equal and their directions are equal
• Same magnitude, same direction are “like” vectors
• Same magnitude, different directions are “unlike” vectors
• Same direction, different magnitude are “like” vectors
• 2 vectors that are parallel, but in opposite directions, are “unlike” vectors

The Negative of a Vector

• For a vector a, the vector -a has the same magnitude but an opposiute direction

$-\overrightarrow{AB}=\overrightarrow{BA}$

Scalar Multiplication

• Given a vector $a$, $2a=a+a$
• For a vector a, and positive scalar $k$(i.e., a positive real number), the vector ka is the vector with the same direction as a and magnitude k|a|
• For a negative $k$,$ka=k|-a|$

Subtracting Vectors

• Think of $a-b=a+(-b)$

$\overrightarrow{AB}+\overrightarrow{BC}-\overrightarrow{DC}=\overrightarrow{AD}$

The Zero Vector

• The zero vector $0$ has magnitude 0 and an undefined direction

Vectors in Component Form

• Any 2D vector can be resolved into a sum of horizontal and verticale components, written as $a\underline{i}+b\underline{j}$ where i and j are unit vectors
• Vectors in component form can be added by adding their components and simplifying
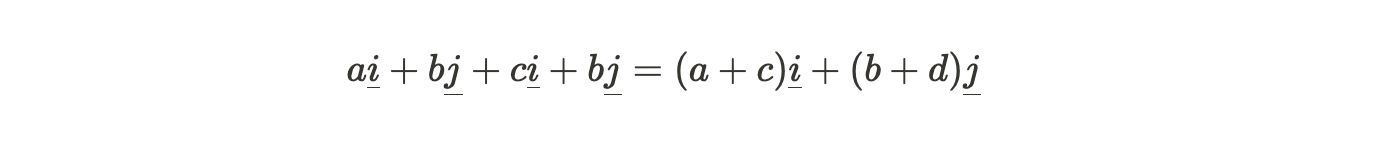
• A vector v can be written in component form as
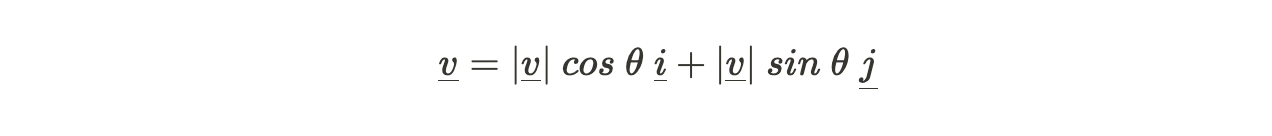
• Given a vector $\underline{v}=a\underline{i}+b\underline{j}$:
• $|\underline{v}|=\sqrt{a^2+b^2}$ -
• $tan\theta =\frac{b}{a}$
• Your calculator will evaluate this with an angle between $-90˚$and $90˚$
• This may not match the quadrant of the vector! If not, add $180˚$
• If the vector is in the 4th quadrant, your calculator will give a negative angle. Add $360˚$to get the equivalent positive angle

Unit Vectors

• Vector that is the same as another with a magnitude of 1
• $\frac{1}{|\underline{v}|}\underline{v}$

Vector Equations

• Vector questions can involve setting up equations and solving them
• Remember, 2 vectors are only equal if their magnitude and direction are equal
• Equivalently, 2 vectors in component form are equal if and only if their components are equal
• $ai+bj=ci+dj$ if and only if $a=c$ and $b=d$
• This means that solving equations with vectors in component form usually incolve equating components

Position Vectors

• Vector used to represent the position of a point relative to the origin (in the Cartesian plane when working in a 2D space)

$\overrightarrow{AB}=-\overrightarrow{OA}+\overrightarrow{OB}$

Multiplication of Vectors

• There are various different ways you could define the product of 2 vectors
• The scalar/dot product of 2 vectors *a and b is $a\cdot b=b\cdot a=|a||b|cos(\theta )$
• $\theta$ is the angle between vectors arranged tail to tail or nose to nose

$a\cdot a=|a{|}^2$

$a\cdot (\lambda b)=\lambda a\cdot b$

$a\cdot (b+c)=a\cdot b+a\cdot c$

${(}_b^a)\cdot {(}_d^c)={(}_{bd}^{ac})$

• $a\perp b$ if and only if $a\times b=0$

Scalar Projections

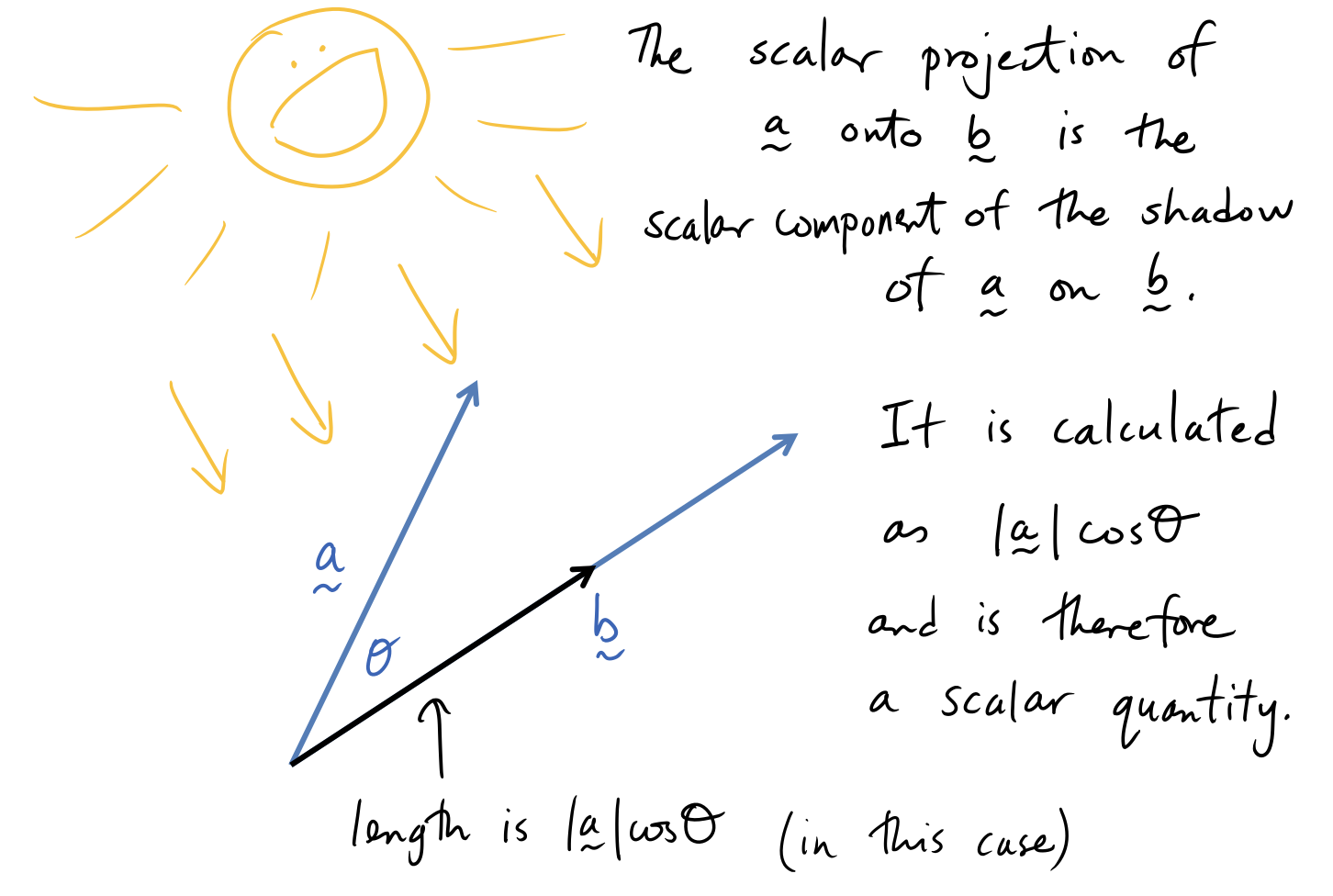
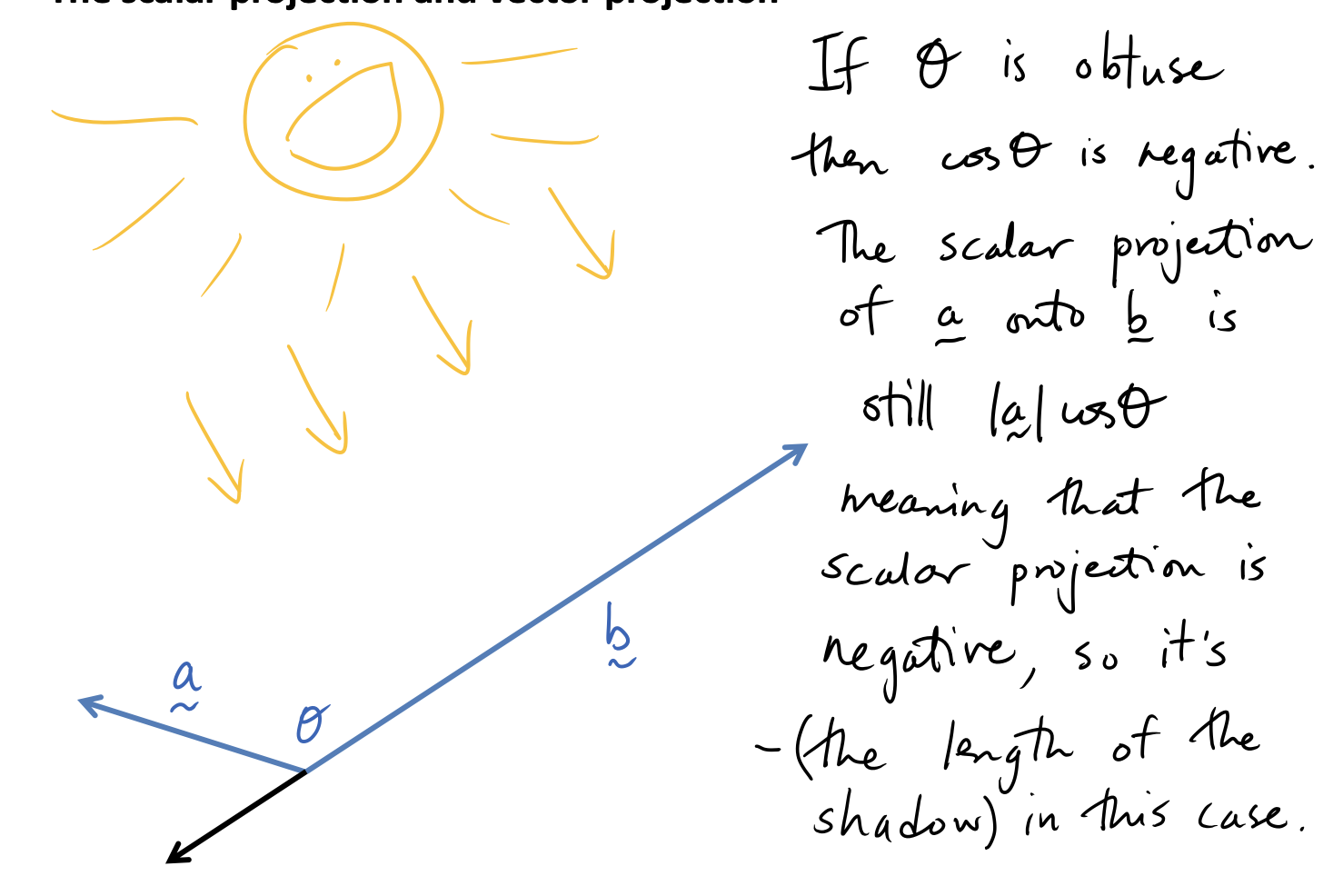
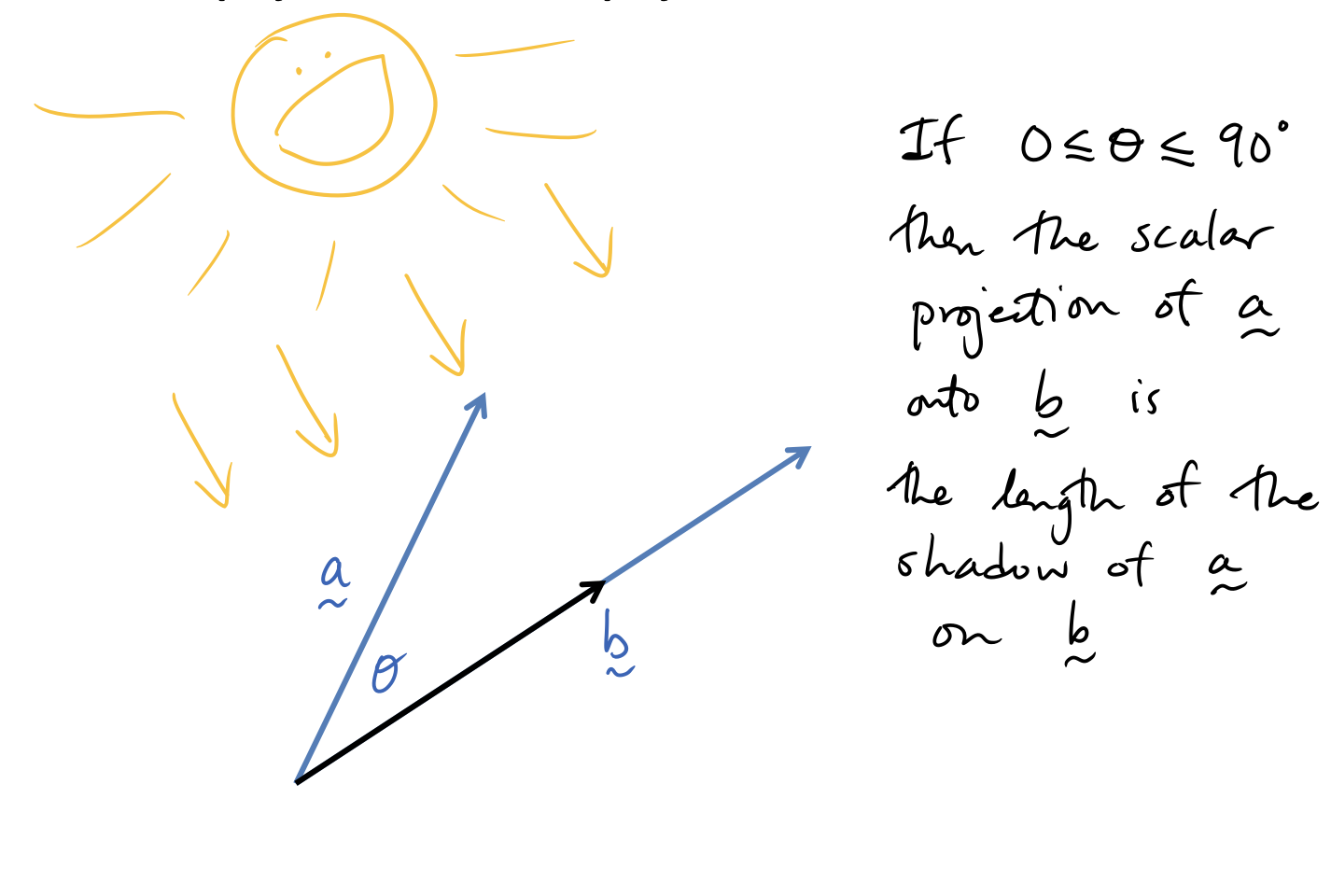
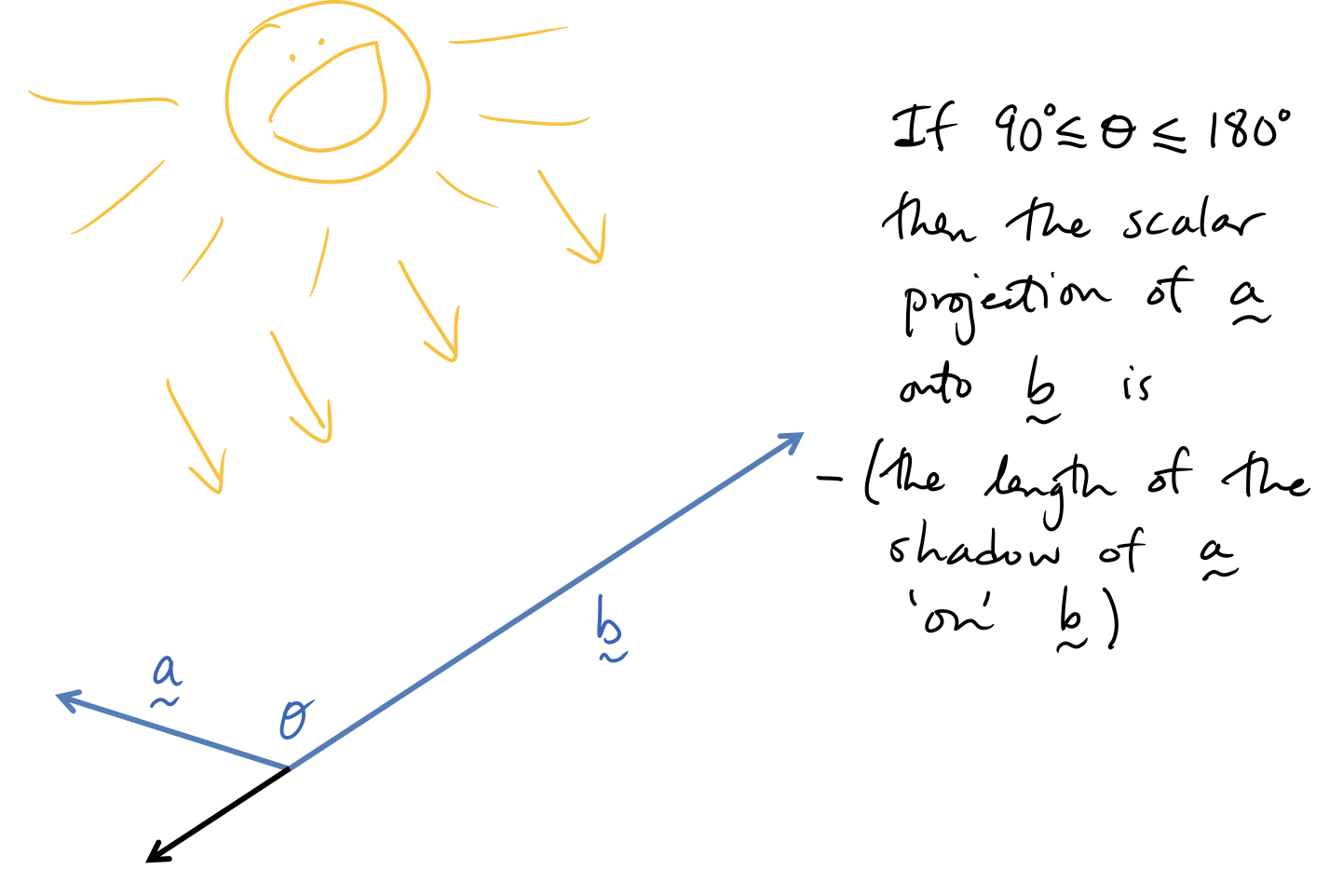
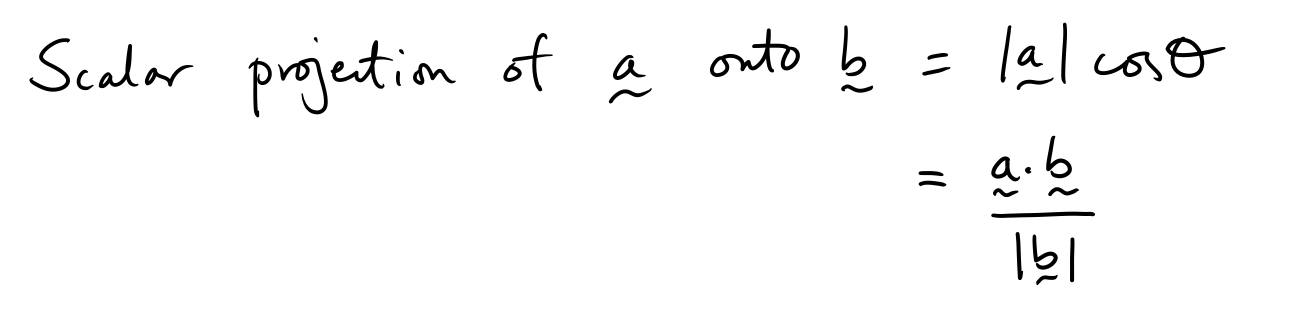
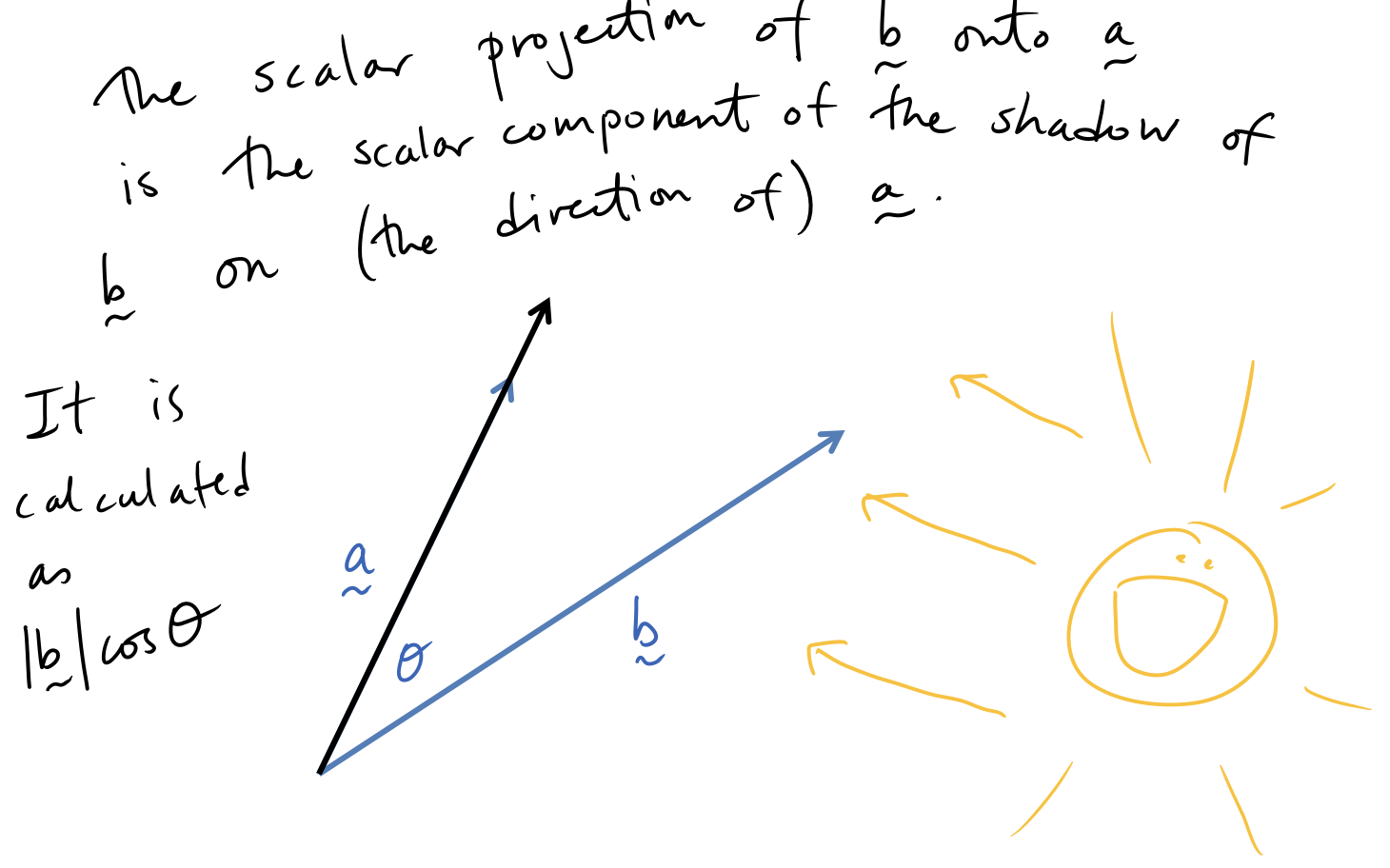
Vector Projections

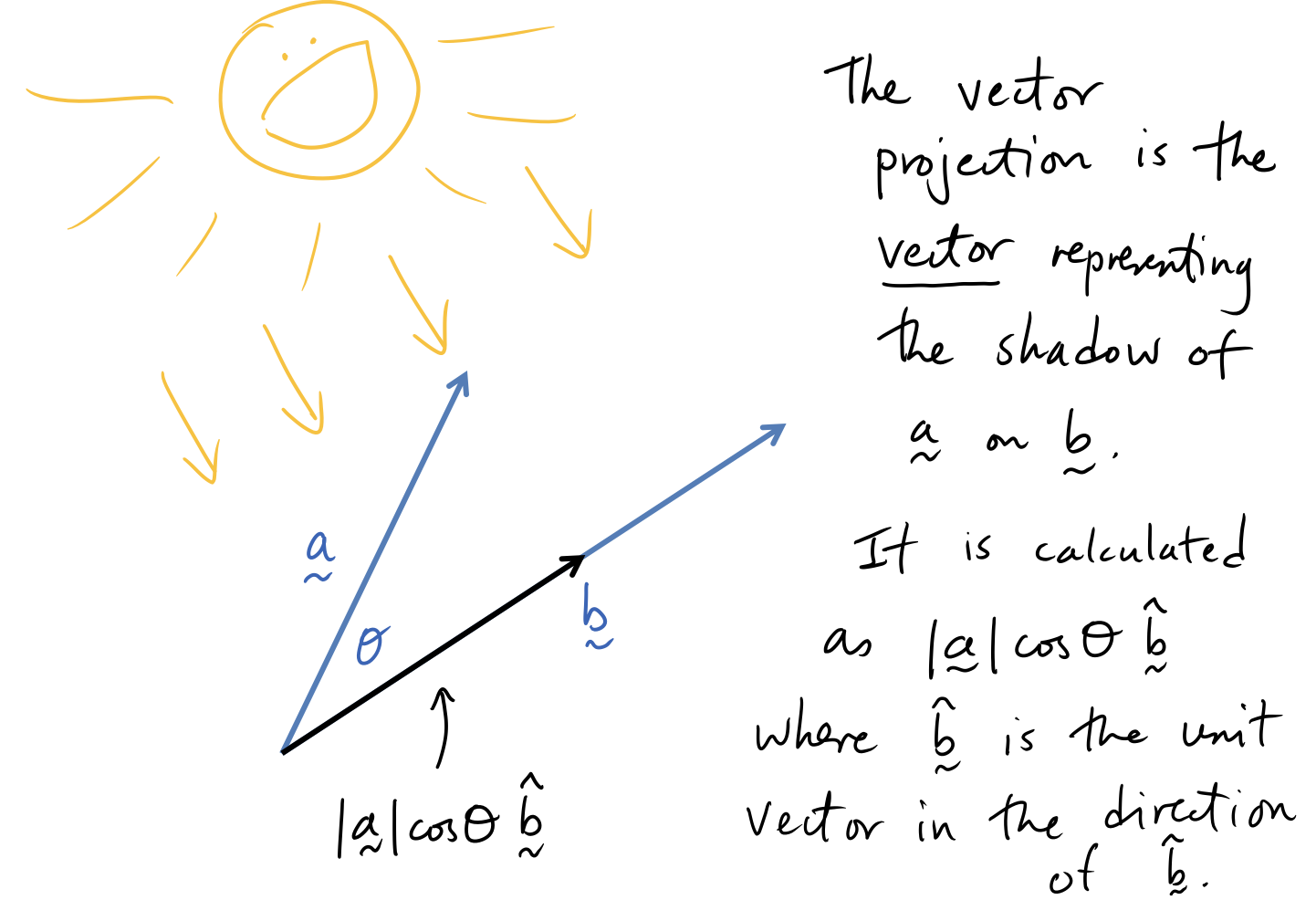
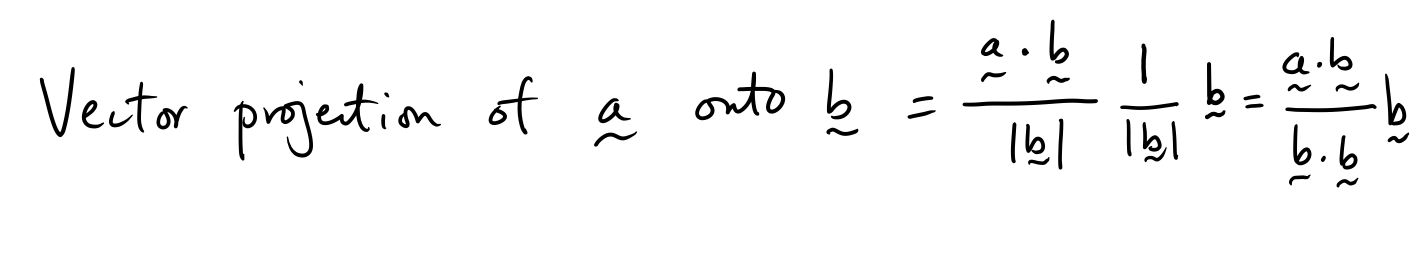
Geometric Proofs using Vectors

• Facts of vector algebra you can use:
  • a = b if and only if a and b have the same magnitude and direction
  • -a has the same magnitude as a but the opposite direction
  • For a scalar $\lambda >0$, $\lambda \overrightarrow{a}$ has magnitude $\lambda |a|$ and the same direction as a
  • If $a=\lambda b$, then if $\lambda >0$ , a and b are like parallel vectors; otherwise, if $\lambda <0$, a and b are unlike vectors
  • Vectors can be added with a triangle of vectors
  • $a-b=a+(-b)$
  • If $\lambda$ is a scalar, then $\lambda (a+b)=\lambda a+\lambda b$
  • $a\perp b$ if and only if $a\times b=0$

Relative Vectors

• For this, we use the concept of position vectors
• The position of Vector A relative to Vector B = ${}_a{p}_b=a-b=\overrightarrow{A}-\overrightarrow{B}$
• The velocity of Vector A relative to Vector B = ${}_a{v}_b=v_a-v_b$