12-05-2023 Spec problems I could solve that edward couldn't

go back

Proof by Counterexample

$\forall n\in \mathbb{N};2n^2-4n+31\in P$ For this, we must show that there exists a natural number $n$, such that $2n^2-4m+31$ is not a prime number, i.e. is a composite number. We must thus use proof by counterexample for this. All single-digit natural numbers come to mind, but we can see that they all equal prime numbers if we input them into the equation. 11, 12 and 13 also do not work, so we use 14. From this, we can see that if: $n=14\therefore 2n^2-4n+31=2(14{)}^2-4(14)+31=2(196)-42+31=381$ 381 is divisible by 3, as they add to give a multiple of 3. Thus, we can say the proof above is false and has been disproven

Edit: Athu told us we could’ve just used 31, so now we feel like idiots

Geometry Proofs

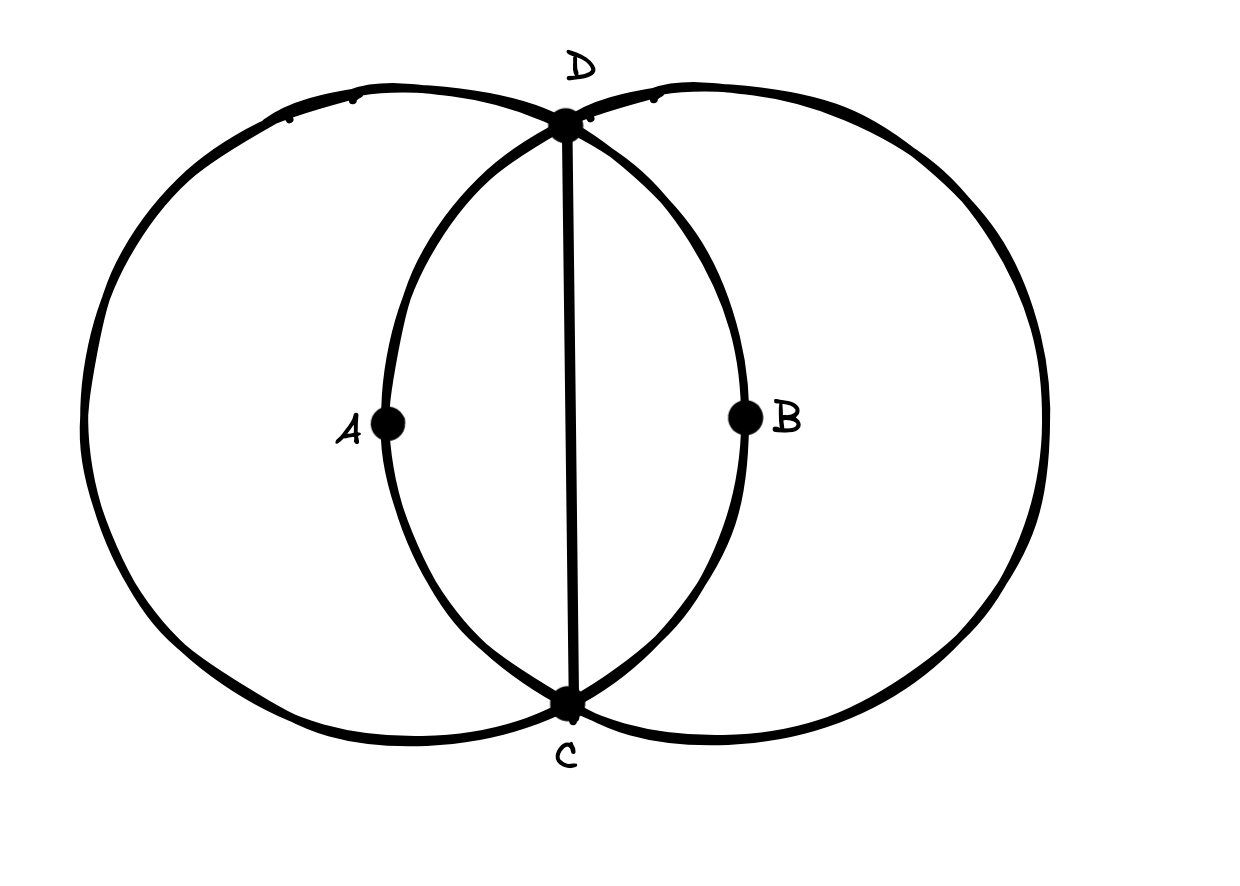
Two circles of radius 12.6 cm, with centres A and B are shown above, have a common chord CD. Determine, with justification, the length CD.

So, we know what the radius is (12.6 cm). However, what does this actually tell us? From this, we can deduce that length AB, AD, AC, BD, and BC are all equal to 12.6 cm, as they are all radii. Furthermore, by drawing the line AB into the diagram, we now have a right angled triangle, like so.

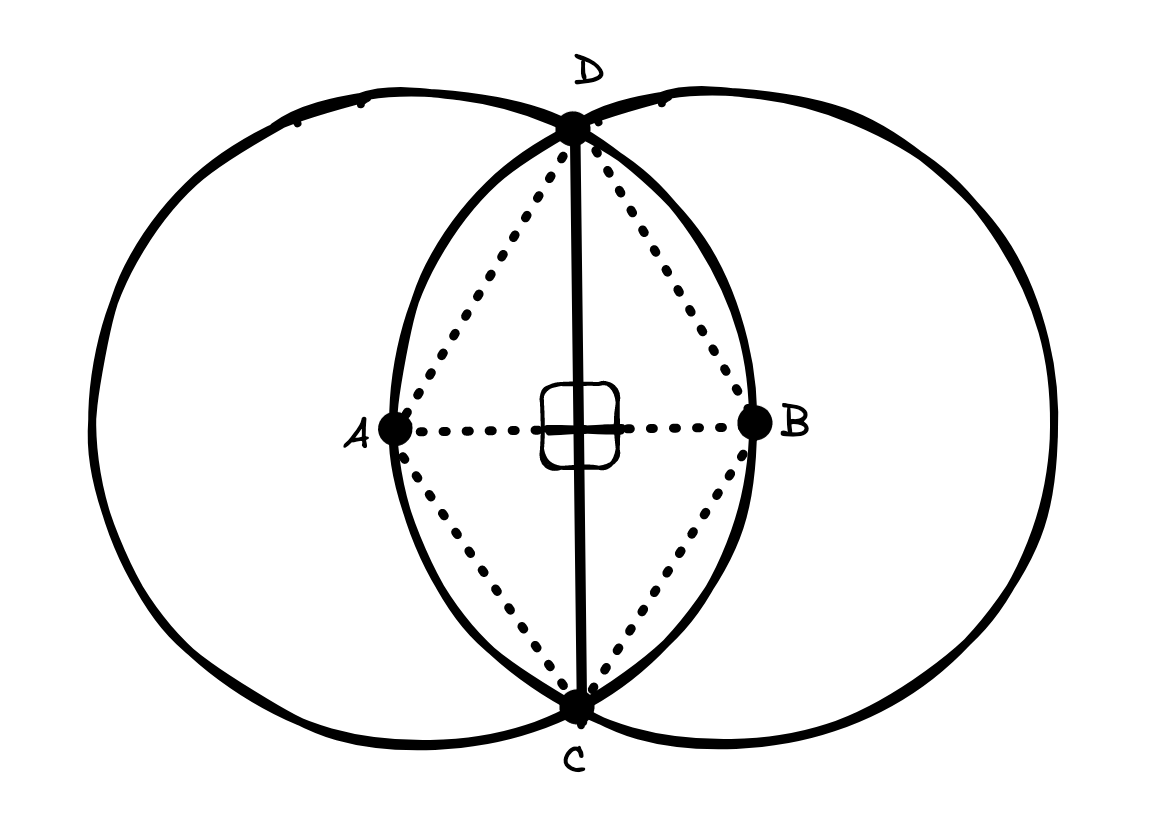
In addition, we can see that the chord CD bisects AB, so now we know that one side of the triangle is 12.6 cm, and the other is 6.3 cm (12.6 cm divided by 2).

From this, we use the Pythagoras theorem, or $a^2+b^2=c^2$, to show that: $6.3^2+c^2=12.6^2\therefore c=\sqrt{12.6^2-6.3^2},c=10.91$ , where c is equal to half the length of chord $CD$.

So now we know that c is equal to 10.91. However, we know that this is only half of chord $CD$, so we must multiply it by 2. And through this, we deduce that $2\times 2\times 10.91=21.82$ . Thus, the length of chord CD is 21.82 cm.