The Theory of Proof

• Basically a mathematical way of proving a statement
• E.g., If a is even and b is even, prove that a+b is even
• We must use notation, and definitions

Notation	Set
$\mathbb{R}$	Real Numbers, all rational and irrational numbers
$\mathbb{Q}$	Rational numbers, all numbers that can be expressed as a fraction
$\mathbb{Z}$	Integers, all whole numbers
$\mathbb{N}$	All natural numbers, i.e. all positive integers. Does not include 0

• If n is even, write:
  • Let $n=2k,k\in \mathbb{Z}$
• If n is odd, write:
  • Let $n=2k+1,k\in \mathbb{Z}$
• If n is rational, write:
  • Let $n=\frac{p}{q};p,q\in \mathbb{Z};gcd(p,q)=1$
• If n is divisible by d for some integer d, write:
  • Let $n=dk,k\in \mathbb{Z}$
• ALWAYS INCLUDE THE SET IT IS IN, E.G. $k\in \mathbb{Z}$
• THIS IS VERY IMPORTANT, YOU WILL LOSE MARKS IF YOU DO NOT DEFINE THE SET
• NEVER ASSUME WHAT YOU WANT TO PROVE. THIS IS A FALSE PROOF, AND WILL COST YOU MARKS
• ALWAYS WRITE “QED” AT THE END OF EVERY PROOF
  • This is Latin for “thus it has been proven”, and shows that you have completed your proof

Some Definitions on Proof

Given a true conditional statement, If A then B:

• The converse may or may not be true: If B then A
• The inverse may or may not be true: If not A then not B
• The contrapositive is always true: If not B, then not A

Direct Proofs

• A proof that is very logical
• You are given an assumption, and asked to prove something
• “If A, then B”

1. Assume that A is true
2. Show that B must follow as a consequence

Proof by Contraposition, or Contrapositive Proofs

• The contrapositive of a true conditional statement (If A then B) is always true
• Contrapositive is: If not B, then not A
• Contrapositive of “A and B” is “not A or not B”
• Contrapositive of “A or B” is “not A and not B”

1. Write as “If not B then not A”
2. Assume that “not B” is true
3. Show that “not A” must follow as a consequence
4. Since it is a contrapositive statement, then “If A then B” is also true

Equivalence Proofs

• A proof that has “if and only if” in the statement
• “A if and only if B”
• Saying that “If A, then B” and “If B, then A”

1. Show that if A is true, B must follow as a consequence
2. Show that if B is true, A must follow as a consequence

Proof by Contradiction

• Basically a false proof
• We try to prove the opposite of what we are told to prove
• For example, if we are trying to prove “If A then B”, we try to prove “If A then not B”
• We show that this is false, or cannot make sense, and that “If A then B” is actually true, as our proof is incorrect
• We usually do this by assuming that a number is irrational, then showing that it is rational

1. Write as “If A then not B”
2. Assume that this is true, that “If A then B” is false
3. Show that this leads to an impossible conclusion
4. “The negation of this conjecture is incorrect as it contradicts…”
5. Then the conjecture must be true

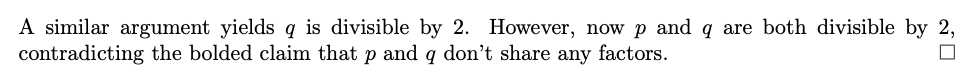
Recurring Decimals as Fractions

• Sometimes, you’ll be asked to represent recurring decimals as fractions
• When that happens, define the decimal as x
• Multiply the decimal by a multiple of 10, until it has a digit that is repeated, in its tens and ones digit. We’ll call this multiple k
• Multiply the decimal by a multiple of 10, until it only has recurring decimals
• Take mx from kx, and this will eliminate the recurring decimals. We’ll call this y
• This can be represented as (k-m)x = y
• $x=\frac{k-m}{y}$