Vector Revision

go back

1. Scalar quantities have only magnitude (e.g. speed, distance)
2. Vector quantities have direction and magnitude (e.g. force and velocity)
3. Vectors are represented by arrows indicating their magnitude and velocity
4. A negative vector value means direction is reversed
5. Vectors can be added or subtracted
6. The resultant of 2 vectors can be graphically by
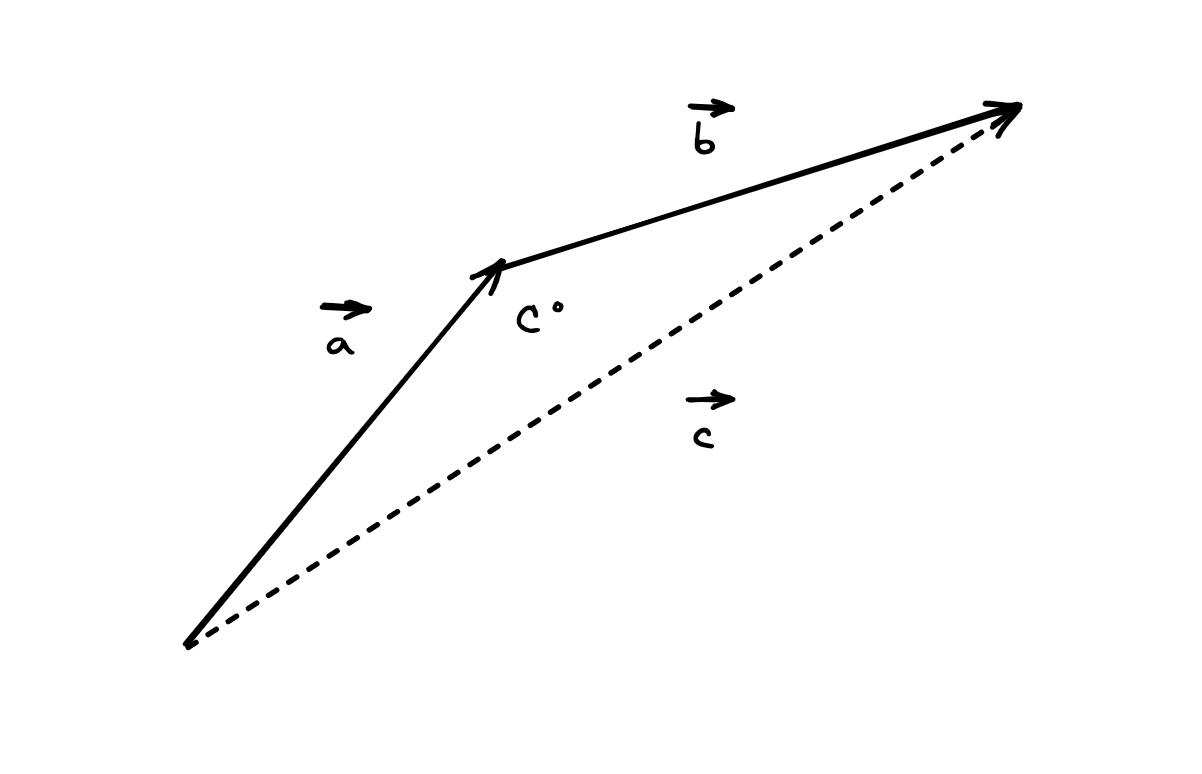
   1. Joining the 2 vector arrows “head to tail” - the resultant is the arrow drawn from the first tail to the second head. This gives a vector triangle
      1. 
   2. Drawing a parallelogram by using the 2 vectors as adjacent sides - the diagonal is the resultant. This is most useful for concurrent (acting at the same point) forces
      1. 
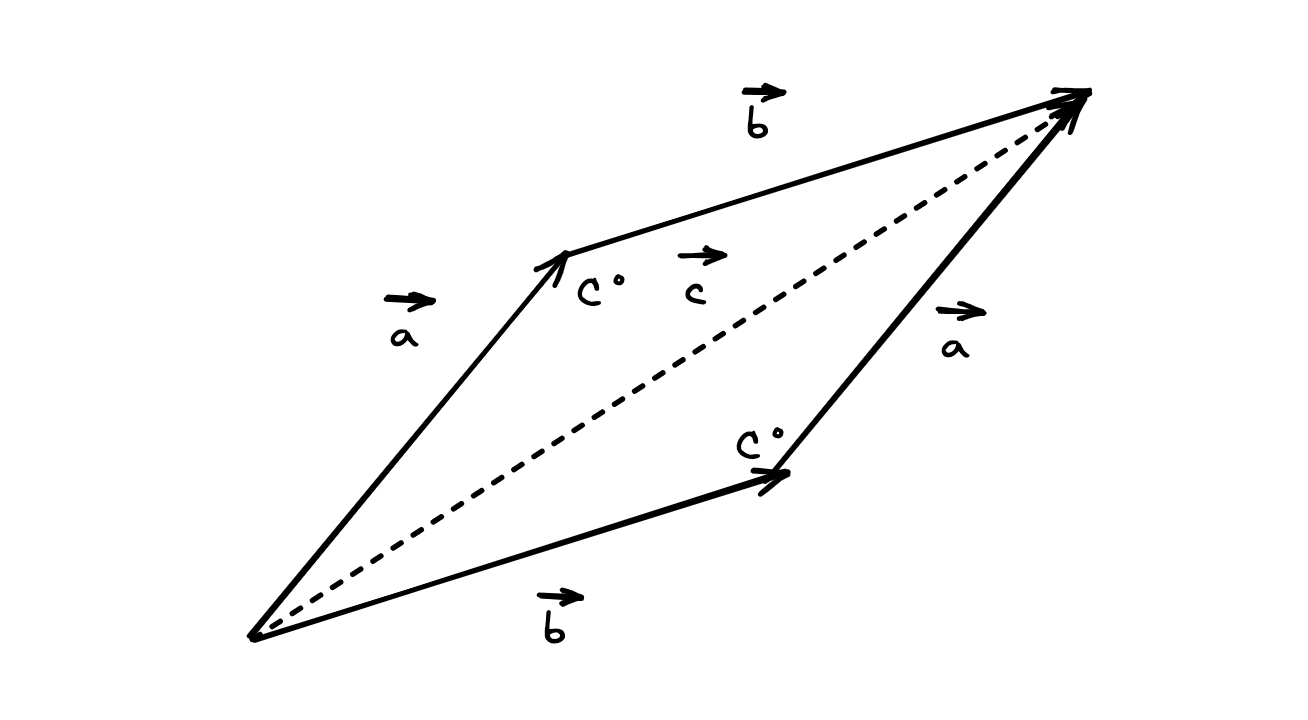
   3. The triangle and parallelogram methods work for vectors at any angle, not just 90˚
   4. To find the resultant you can use the sine or cosine rule
   5. The parallelogram method is better at showing what is actually happening
7. The magnitude and direction of the resultant of 2 vectors can be calculaed using the sine/cosine rules (given on SCSA Data Sheet) or the Pythagorean formula (for vectors acting at 90˚)
   1. For the triangles above:
   2. Cosine Rule to find the magnitude of side c: $c^2=a^2+b^2-2ab\times cos(C)$
   3. Sine rule to find the angle it makes from the x axis. They’ll usually give you another angle, to add to this value, as this is not connected to the x or y axis: $\frac{sin(A)}{a}=\frac{sin(B)}{b}=\frac{sin(C)}{c}$
   4. For a right angled triangle, where c is the hypotenuse and a and b are other sides: $a^2+b^2=c^2$
8. Subtraction of vectors
   1. This is the same as finding the change ($\Delta \text{v}$) in a vector quantity
   2. To subtract one vector (A) from another (B), simply add its opposite
   3. Order is important - the subtracted one must be added as an opposite
   4. $\Delta \text{v}=v-u=v+(-u)$
      1. v = final velocity (speed and direction)
      2. u = initial velocity (speed andd direction)
9. Vector components
   1. A vector can have effects in directions other than its own direction (but not at 90˚ to its own direction)
   2. These angular effects are called components
   3. The magnitude of a component can be found by $C=V\cos \theta$, where $\theta$ is the angle in between the vectors
   4. Any vector can be resolved into 2 rectangular (perpendicular) components, whose magnitude can be found use trigonometry
   5. Note: you can also find it with this, where $\theta$ is the angle it makes with the positive x-axis
      1. $V\cos \theta$ as the horizontal component
      2. $V\sin \theta$ as the vertical component
10. The equilibrate of 2 forces is equal in magnitude but opposite in direction, to their resultant